サマリーROC曲線 (Summary Receiver Operating Characteristic Curve)

サマリーROC曲線
(Summary Receiver Operating Characteristic Curve)

サマリーROC曲線とは？

同一疾患に対する診断に用いられる検査が複数以上ある場合に、その検査特性を知った上で用いることが必要である。このため、様々な研究で求められた感度、特異度などが有用な情報として臨床で用いられている。
しかし、これらの有用な情報も、対象となった患者の内容や検査が施行された医療機関の機能(一般の診療所や病院などのプライマリ・ケア施設や紹介患者が主の二次・三次医療機関)によって、さらには用いられた陽性(positive)・陰性(negative)の判断値(cut off value)によって大きく異なる場合が多い。検査結果の陽性基準(判断値：カットオフ値)が変化する時にROC曲線はグラフ上に診断検査における真陽性と偽陽性の比を表すものであるが、そのような異なる検査特性が示された複数の研究を用いてより普遍性が高いと考えられる検査特性を得るために、用いられるのがMosesLEらによって提唱されたサマリーROC曲線(Summary Receiver Operating Characteristic Curve：SROCC)の概念である。研究間の検査特性の変動の一部は、異なったカットオフ値を用いたことが原因であると仮定している。

概要を以下に紹介すると

ある検査についての検査特性が次のように２×２テーブルで表される場合に、次の項目は以下のように表すことができる。

２×２テーブルのそれぞれのセルが０にならないように0.5を加えている。

この真陽性率(TPR)と偽陽性率(FPR)の判断値に依存した関係を表したものがROC曲線であるが、TPRとFPRの関係は増減が一致しているため、下記のようなlogit変換を行うことで、線型の回帰式が求められることが経験的にわかっている。すなわち、

P: 確率あるいは比率
今、U,VをFPRとTPRのlogit変換を行ったものとすると、一般的には

と表される。
いま、判断値γを変化させて検査特性の変化をみた際に、以下のような式でそれぞれが表される場合には、

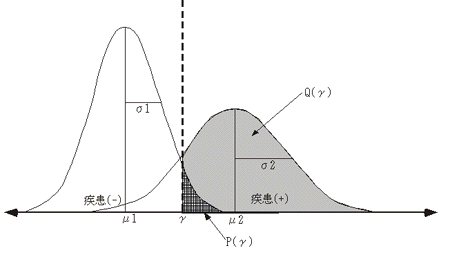
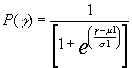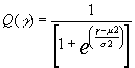
ロジスティック分布に従っていることになり、U軸とV軸にとって(U,V)をプロットすると直線になることがわかっている。
今、それぞれの研究で示された２×２tableの数値を当てはめると

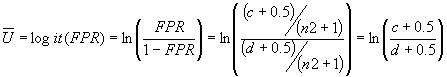
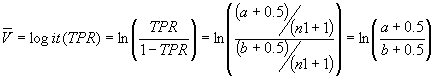
となるが、この(

)の観察値になるため、曲線に戻すことが可能である。

σ1=σ2の場合には、(U,V)をプロットした直線は45°になることがわかっているため、さらにV―UをＹ軸に、V＋UをX軸にしてプロットすると、σ1=σ2の場合には傾きが０の直線になる。

そこで

(Sum)＝

＋

(Difference)＝

―

として表すとそれぞれの研究から求められた点

_i、

_i　　　i∈Ｎ(見いだされた同様の研究総数)から

Ｄ＝ A ＋ BS

とした直線回帰式をもとめることができる。
(この回帰式を求めるには、一般的な最小二乗法以外に、重みづけ回帰やロブスト回帰などから求められる。)

その求められた係数Bと切片Aから以下のようなROC曲線を描くことができる。

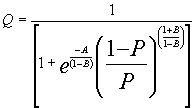
この場合に注意すべきことは、Ｄが非常に中心から離れた点(

、

)は、その回帰直線の係数Ｂに大きな影響を有することである。しかし、非常に大きな、あるいは非常に小さな(FPR、TPR)の点は、臨床的には適用されないことが多いため、適切な範囲の点について考慮し、それから外れる点を入れるか、除くかを検討する必要がある。この範囲を設定した場合にはSROCCもその範囲内で描くことになる。

例

信頼区域
B=0である場合には、SROCCは、

の式から

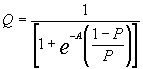とAに依存した関数となり、Aの信頼区間がAL(信頼区域下界)AU(信頼区域上界)にある場合、ROC曲線も信頼区間を示す曲線を以下のような形で表される

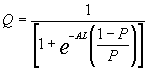　と　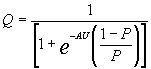　の間にあることになる。

サマリーROC曲線の活用

1)同一疾患に用いられる複数の検査の比較が可能
前述のように、通常のROC曲線の場合には、曲線下の面積が検査特性の優劣を評価するために用いられるが、明らかに低い特異度(偽陽性が大きい)や感度(偽陰性が大きい)の研究の箇所は臨床上では適用されないため、サマリーROC曲線の構築の際には、用いられないことが多い。このため、曲線下の面積が用いられない場合が多いが、この場合には、ROC曲線とTPR=(1-FPR)、言い換えれば感度＝特異度の線が交わる交点の位置でその優劣を比較することが可能である。この値が１となる点が左上のコーナーになり、値が１に近づけば近づくほど、検査特性のよい検査となる。従って、この値を比較することで、優劣の比較が可能となる。この比較で統計的な有意差をみるためには、以下の式で求められた値を正規分布表(少なくとも10研究以上から構築されたROC曲線)に当てはめることが可能である。

Q値とその標準誤差(SE)は次の式から求められる。

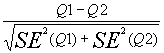
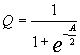
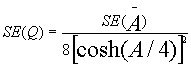
(同一の被検者が含まれないなど、複数の検査が独立の場合に適用)
そのほかに、Bが０である(すなわち、TPR=(1-FPR)に対して対称である) 場合には、それぞれの研究から出されたDについて検定を行うことも可能である。

2)適切な診断特性値(尤度比)の決定
通常のROC曲線と同様に、サマリー曲線から適切な感度・特異度を見いだすことも可能である。この診断特性値(尤度比)は検査自体の危険性や侵襲が無視できる場合には、診断に引き続く治療によってもたらされるメリット(Benefit)と危険性(Cost)によって決定される。

　　Ｓ：ROC曲線の接線の傾き

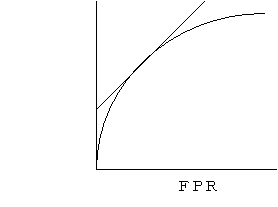
このBenefitとCostは、判断分析によりなされるが、単純に考えると、治療が例えば手術のような侵襲の強いものであればより偽陽性の少ない方に、すなわち、特異度が高い方になるため、ROC曲線の接線(スロープ)の傾きは急峻になる。特に侵襲が強くなく、また、治療によるメリットが大きい場合には、傾きは緩やかに感度の高い方へ移動する。

3) 極端な飛びはね値(Extreme Outlier)の検出
同じ検査特性をみた研究でも、中には他の研究の特性とはかけ離れて良いもの、あるいは悪いものが含まれることがある。その際に、その研究を検出することが可能であり、また、どうしてそのような飛びはね値になったのかといった検討(有病率の異なる集団など患者層が異なる、診断基準が異なる、研究方法が異なるなど)が必要になる。

¹ 同様の検討は、Karduanら、Inouyeらによってもなされている。