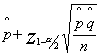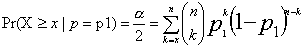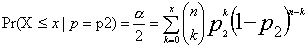感度・特異度の信頼区間の求め方
正規分布を仮定した場合
感度・特異度(p)が0あるいは1に近い場合は正規分布を仮定できないため、誤差が大きくなるので勧められない。
Rule of Thumb (経験則)として
サンプル数:N
感度あるいは特異度:
p
とした場合に、
NpとN(1−p)が5以上の場合に適用することが可能とされている。
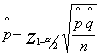 〜
〜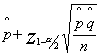
で
95%信頼区間の場合、Z1-α/2=1.96
99%信頼区間の場合、Z1-α/2=2.58
として計算する。
二項分布を仮定した場合
感度・特異度(p)が0あるいは1に近い場合で正規分布として仮定できな場合には、二項分布を仮定する。
この場合には、次の式を満たす範囲で信頼区間が求められる。
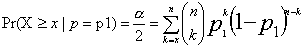
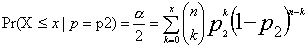
一般的には、この計算が煩雑であることから、図より求める。
その方法は、下記のような図において、pが0.5より小さい場合には、下の横軸で、0.5より大きい場合には、上の横軸で、そのpの推定値に該当する確率をみつけ、そこから垂直に線を引く。
その垂直線が、サンプル数(N)の曲線と交わる点から水平線をひいて左側あるいは右側の縦軸との交点からその信頼区間の値を読みとる。
<例>
今、サンプル数が20で、感度が0.95の場合の信頼区間を求めると、
下図のようになる。
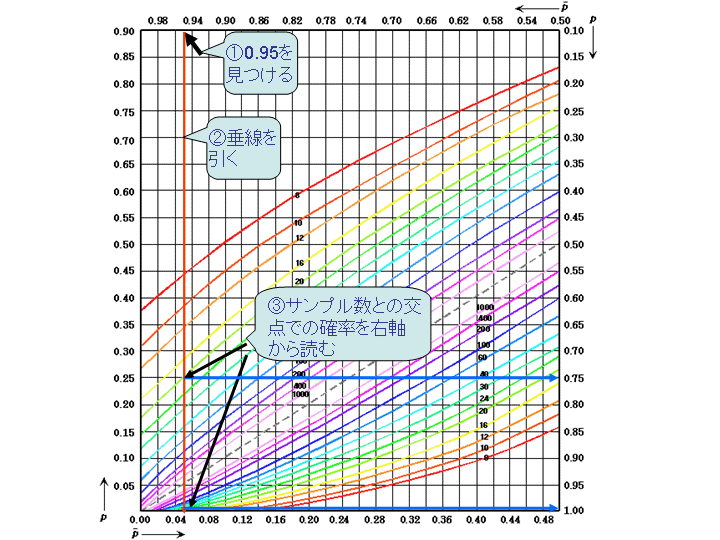
ここで、右軸(p値が0.5より大きい場合には右軸、小さい場合には左軸を読む)との交点は、0.75と0.99ぐらいとなるので、信頼区間はこの範囲となる。
95%信頼区間図の表示
99%信頼区間図の表示
95%信頼区間図の印刷用
99%信頼区間図の印刷用
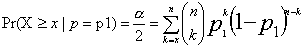
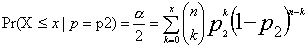
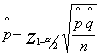 〜
〜